Rapalski ugovor Galerija | Poveznice | Izvori | Navigacijski izbornikHrvatska enciklopedija (LZMK) - Rapalski ugovorOpća i nacionalna enciklopedija - Rapallski ugovor
Međunarodni ugovoriPovijest prve JugoslavijeItalija između dva svjetska rata
RapalluGenoveKraljevine SHSKraljevine ItalijeSlobodne Države RijekeHabsburgovacaLondonskim ugovorom 1915.mirovne konferencije u Parizu 1919.–1920Milenko VesnićAnte TrumbićKosta StojanovićGiovanni GiolittiCarlo SforzaIvanoe BonomiTrstGoricaGradiškaKranjskeIstraKastavZadarCresLošinjLastovoPalagružaSlobodna Država Rijekatalijanskog jezikaHrvatskaII. svjetskog ratazadarskogSlobodna Država RijekaKraljevine SHS
Rapalski ugovor
Prijeđi na navigaciju
Prijeđi na pretraživanje
Potpisivanje Rapalskog ugovora
 Ovo je glavno značenje pojma Rapalski ugovor. Za ugovor između Weimarske Njemačke i Boljševičke Rusije, pogledajte Rapalski ugovor (1922.). |
Rapalski ugovor[1] ili Rapallski ugovor,[2] sporazum koji su u Rapallu, gradiću blizu Genove, 12. studenog 1920. potpisali predstavnici Kraljevine SHS i Kraljevine Italije, nakon pregovora koji su započeli 9. studenog. Njime su bile određene međusobne granice tih država, bilo je dogovoreno stvaranje neovisne Slobodne Države Rijeke te zajedničko nastupanje protiv svih pokušaja restauracije dinastije Habsburgovaca. Rapalskim ugovorom nastojala su se riješiti mnogobrojna otvorena pitanja oko granica dviju država, koja su postavljena Londonskim ugovorom 1915., a nisu bila riješena za mirovne konferencije u Parizu 1919.–1920. Pregovori u Rapallu održani su u nepovoljnom međunarodnom političkom okruženju za Kraljevinu SHS zbog sve veće sklonosti britanske, francuske i američke diplomacije da popusti talijanskim zahtjevima.[1]
Glavni pregovarači na strani Kraljevine SHS bili su premijer Milenko Vesnić, ministar vanjskih poslova Ante Trumbić i ministar financija Kosta Stojanović, a s talijanske strane Giovanni Giolitti, Carlo Sforza i Ivanoe Bonomi. Talijanski pregovarači jasno su dali do znanja da bi se talijanski prijedlog trebao prihvatiti, a u suprotnom je Italija bila spremna sama uspostaviti granice predviđene Londonskim ugovorom. Time je delegacija Kraljevine SHS bila prisiljena potpisati nepovoljan ugovor, kojim su Italiji pripojeni Trst, Gorica, Gradiška i dio Kranjske, Istra (osim dijela općine Kastav), grad Zadar, otoci Cres i Lošinj, Lastovo i Palagruža, te je stvorena Slobodna Država Rijeka. Rapalskim ugovorom talijanskoj nacionalnoj manjini u Kraljevini SHS bilo je omogućeno pravo optiranja za talijansko državljanstvo, uporaba talijanskog jezika i sloboda vjeroispovijesti, a hrvatskoj i slovenskoj nacionalnoj manjini u Italiji nisu dana nikakva zakonska jamstva koja bi omogućila njihovu nacionalnu opstojnost.[1]
Zbog općega nezadovoljstva u Kraljevini SHS, ugovor nikada nije bio razmatran u Narodnoj skupštini, već je 26. lipnja 1921. ozakonjen bez parlamentarne rasprave te je, točno nakon godinu dana, bio potvrđen kraljevom odlukom.[1] Ugovor je velikim dijelom bio rezultat velikosrpske politike usmjerene na nagodbu s Italijom u cilju slabljenja hrvatskog položaja u Kraljevini SHS.[2] Područja koja je Hrvatska izgubila tim ugovorom vraćena su joj nakon II. svjetskog rata.[1][2]
Galerija |
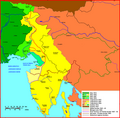
Granice u Istri tijekom XX. stoljeća
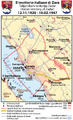
Razgraničenje oko zadarskog područja
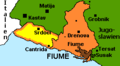
Slobodna Država Rijeka, narančasta i žuta
Konačne granice Kraljevine SHS
Poveznice |
- Londonski ugovor
- Rimski ugovori (1941.)
- Nastanak Kraljevstva SHS
- Hrvatska u prvoj Jugoslaviji
Izvori |
↑ 1,01,11,21,31,4 Hrvatska enciklopedija (LZMK) - Rapalski ugovor
↑ 2,02,12,2 Opća i nacionalna enciklopedija - Rapallski ugovor
Kategorije:
- Međunarodni ugovori
- Povijest prve Jugoslavije
- Italija između dva svjetska rata
(window.RLQ=window.RLQ||[]).push(function()mw.config.set("wgPageParseReport":"limitreport":"cputime":"0.040","walltime":"0.061","ppvisitednodes":"value":151,"limit":1000000,"ppgeneratednodes":"value":0,"limit":1500000,"postexpandincludesize":"value":461,"limit":2097152,"templateargumentsize":"value":84,"limit":2097152,"expansiondepth":"value":4,"limit":40,"expensivefunctioncount":"value":0,"limit":500,"unstrip-depth":"value":0,"limit":20,"unstrip-size":"value":4823,"limit":5000000,"entityaccesscount":"value":0,"limit":400,"timingprofile":["100.00% 39.324 1 -total"," 16.62% 6.536 1 Predložak:Dz"," 16.29% 6.404 1 Predložak:Izvori"],"cachereport":"origin":"mw1266","timestamp":"20190401115721","ttl":2592000,"transientcontent":false););"@context":"https://schema.org","@type":"Article","name":"Rapalski ugovor","url":"https://hr.wikipedia.org/wiki/Rapalski_ugovor","sameAs":"http://www.wikidata.org/entity/Q871407","mainEntity":"http://www.wikidata.org/entity/Q871407","author":"@type":"Organization","name":"Contributors to Wikimedia projects","publisher":"@type":"Organization","name":"Wikimedia Foundation, Inc.","logo":"@type":"ImageObject","url":"https://www.wikimedia.org/static/images/wmf-hor-googpub.png","datePublished":"2006-04-16T13:24:27Z","dateModified":"2017-11-28T10:08:13Z","image":"https://upload.wikimedia.org/wikipedia/hr/d/d7/Potpisivanje_Rapalskog_ugovora.JPG"(window.RLQ=window.RLQ||[]).push(function()mw.config.set("wgBackendResponseTime":104,"wgHostname":"mw1331"););
